Custom Search

back to Kinetics and Equilibrium links

What is Ksp?

^{How does an Ionic Compound dissolve?}

^{The simplest way to describe this is the cation and the anions dissociate (break apart) into individual ions. Note****polyatomic ions stay together.}

^{How do we write a chemical expression of dissolving?}

^{When writing an ionic equation, any subscripts of anions and cations now become coefficients on the product side (right of the arrow). You must include the charges and the phase is now aqueous.}

PbCrO_4(s) <=> Pb^{2+(aq) +} CrO₄^2-(aq)

^{AgCl(s) <=> Ag+(aq) + Cl-(aq)}

CaCO₃(s) <=> Ca²⁺(aq) + CO₃^2-(aq)

BaSO₄ (s) <-->Ba²⁺ (aq) + SO₄^2- (aq)

Practice writing equations-Highlight to reveal answer

Writing the K_sp expression

Used when an ionic compound dissolves into its ions.

  For the reaction:

 

K =	[B]b[C]c
	[A]a

 

Since the concentration of the solid is a constant, it is effectively incorporated into the equilibrium constant:

Determining Ksp from Solubility

***Solubility = X***

There are 4 different versions of an ionic compound dissolving

reaction	Ksp expression	Ksp with X values	Ksp as X
AB <-->  A+  +  B-	Ksp=[ A+]  [ B-  ]	Ksp= [ X] [ X]	X2
AB2 <-->  A2+  +  2B-	Ksp= [ A2+]  [ B-  ]2	Ksp= [ X]  [ 2X  ]2	4x3
AB3 <-->  A3+  +  3B-	Ksp=[ A3+]  [ B-  ]3	Ksp= [ X]  [ 3X  ]3	27x4
A2B3 <-->  2A3+  +  3B2-	Ksp=[ A3+]2  [ B2-  ]3	Ksp= [ 2X]2  [ 3X  ]3	108x5

Let's see how this plays out

Example 1   AgBr   (2 ion salt  ksp =x²⁾

Determine the K_sp of silver bromide, given that its molar solubility is 5.71 x 10¯⁷ moles per liter.

When AgBr dissolves, it dissociates like this:

The K_sp expression is:

K_sp = [Ag⁺] [Br¯]

Putting the values into the K_sp expression, we obtain:

K_sp = (5.71 x 10¯⁷) (5.71 x 10¯⁷) = 3.26 x 10¯¹³

or Ksp= X²

Calculating solubility from Ksp

(2 ion salt  ksp =x²  and X is the solubility)

NORMAL Determine the molar solubility of silver bromide, given that its Ksp= 3.26 x 10¯¹³.

When AgBr dissolves, it dissociates like this:

Putting the values into the K_sp expression, we obtain:

K_sp = [Ag⁺] [Br¯]

K_sp = (X) (X) = 3.26 x 10¯¹³

X²=3.26 x 10¯¹³

X=5.71 x 10¯⁷M

Example 3  (3 ion salt  Ksp= 4x³, X is the solubility in moles/L)

HARDER Calculate the solubility of CaF₂ in g/L (K_sp = 4.0 x 10^-8)

First, write the BALANCED REACTION:

Next, set up the SOLUBILITY PRODUCT EQUILIBRIUM EXPRESSION:

In the above equation, however, we have two unknowns, [Ca²⁺] and [F^-]².  So, we have to write one in terms of the other using mole ratios.  According to the balanced equation, for every one mole of Ca²⁺ formed, 2 moles of F^- are formed.  To simplify things a little, let's assign the variable X for the solubility of the Ca²⁺:

If we SUBSTITUTE these values into the equilibrium expression, we now only have one variable to worry about, X: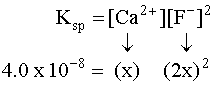

We can now SOLVE for X: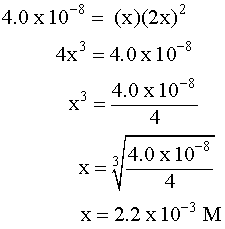

We assigned X as the solubility of the Ca²⁺ which is equal to the solubility of the salt, CaF₂.  However, our units right now are in molarity (mol/L), so we have to convert to grams: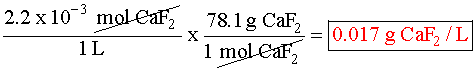

 

1. The solubility of PbCrO₄ is 1.34 x 10^-7 mol/L at 25ºC. Calculate the value of K_sp.

Solution: PbCrO4(s) <=> Pb2+(aq) + CrO42-(aq) Ksp = [Pb2+][CrO42-] Ksp = (1.34 x 10-7) (1.34 x 10-7) Ksp = 1.80 x 10-14

2. The K_sp for AgCl is 1.7 x 10^-10 at 25ºC. What is the solubility of AgCl?

Solution: Let's represent the concentration of Ag+ as "x". Since there will be an equal concentration of Cl-, this can be represented as "x" also. then, AgCl(s) <=> Ag+(aq) + Cl-(aq) Ksp = [Ag+][Cl-] Ksp = [x] [x] Ksp = x2 1.7 x 10-10 = x2 x = square root of 1.7 x 10-10 x = 1.3 x 10-5 mol/L

back to Kinetics and Equilibrium links

Chemical Demonstration Videos